| Greek | Call | Put | |
|---|---|---|---|
| 0 | Price | 4.6150 | 3.3728 |
| 1 | Delta | 0.5695 | -0.4305 |
| 2 | Gamma | 0.0393 | 0.0393 |
| 3 | Theta (daily) | -0.0287 | -0.0152 |
| 4 | Vega (1%) | 0.1964 | 0.1964 |
| 5 | Rho (1%) | 0.1308 | -0.1161 |
Option Greeks
Measuring option sensitivities
finance
derivatives
options
The Greeks measure how option prices change with respect to underlying parameters, essential for risk management and hedging.
1 Abstract
The Greeks are partial derivatives of option price with respect to model parameters. They quantify sensitivity to changes in underlying price (Delta, Gamma), time (Theta), volatility (Vega), and interest rates (Rho). Understanding Greeks is essential for hedging, risk management, and options trading strategies.
2 The Greeks
| Greek | Symbol | Measures | Formula (Call) |
|---|---|---|---|
| Delta | \(\Delta\) | Price sensitivity | \(N(d_1)\) |
| Gamma | \(\Gamma\) | Delta sensitivity | \(\frac{N'(d_1)}{S\sigma\sqrt{T}}\) |
| Theta | \(\Theta\) | Time decay | \(-\frac{S N'(d_1) \sigma}{2\sqrt{T}} - rKe^{-rT}N(d_2)\) |
| Vega | \(\mathcal{V}\) | Volatility sensitivity | \(S\sqrt{T}N'(d_1)\) |
| Rho | \(\rho\) | Interest rate sensitivity | \(KTe^{-rT}N(d_2)\) |
Where \(N'(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\) is the standard normal PDF.
3 Compute (Python)
4 Delta (\(\Delta\))
Delta measures how much the option price changes for a $1 move in the underlying.
- Call delta: 0 to 1 (ATM ≈ 0.5)
- Put delta: -1 to 0 (ATM ≈ -0.5)
- Interpretation: A 0.60 delta call gains ~$0.60 when stock rises $1
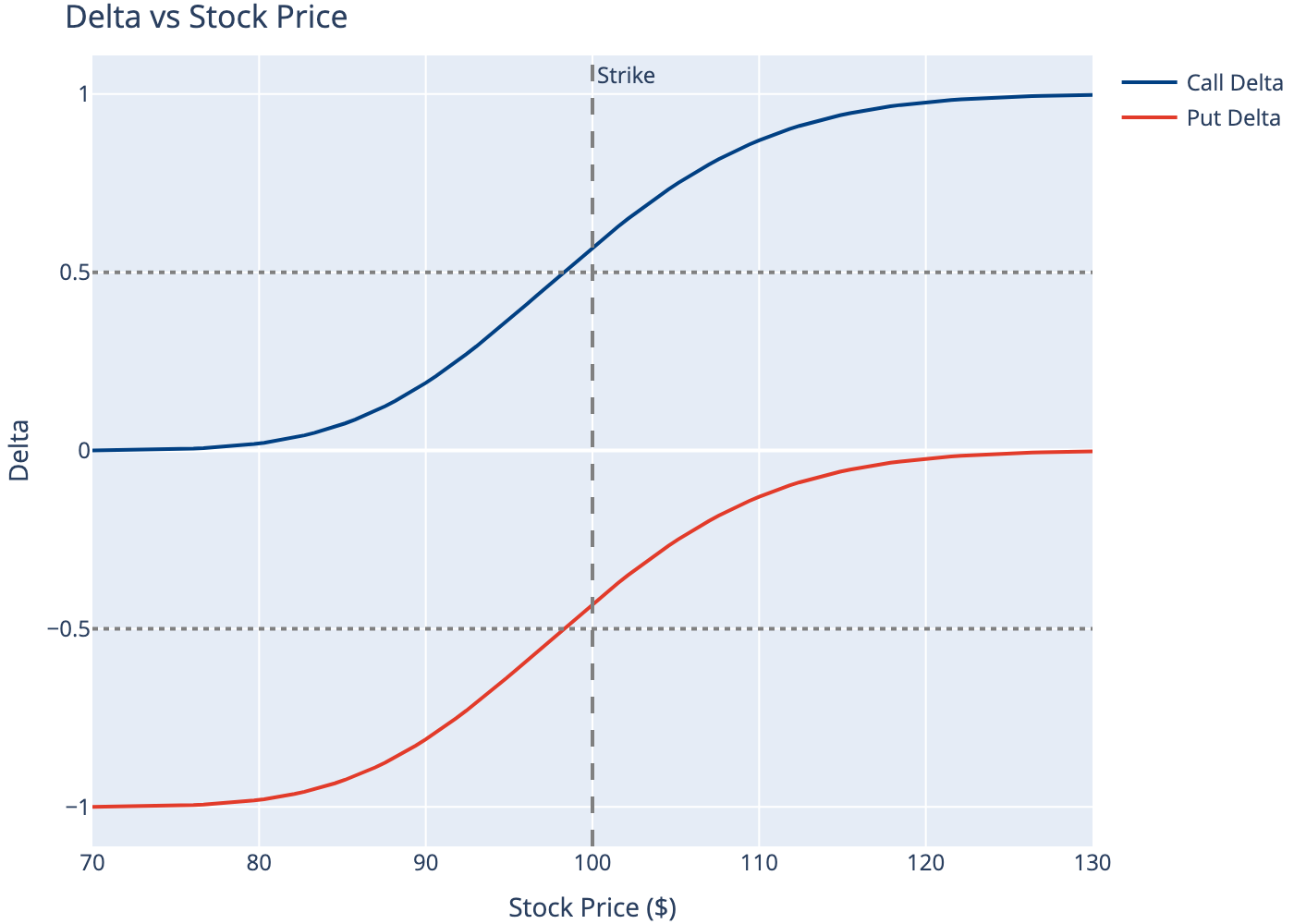
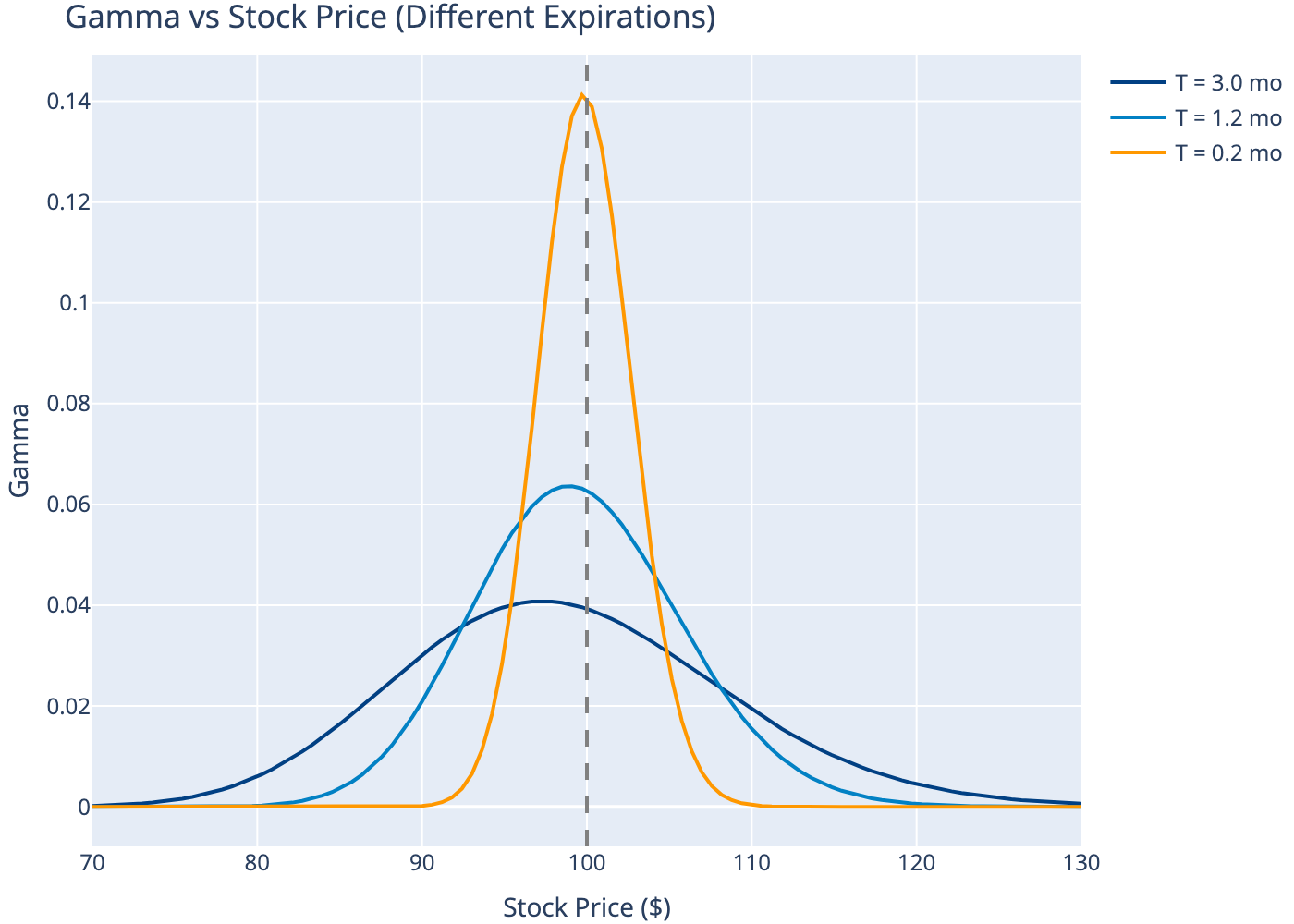
5 Gamma (\(\Gamma\))
Gamma measures how fast delta changes—the “acceleration” of the option price. Gamma is highest for ATM options near expiration.
6 Theta (\(\Theta\))
Theta measures time decay—how much value the option loses each day. Options lose value as expiration approaches, with decay accelerating for ATM options.
7 Vega (\(\mathcal{V}\))
Vega measures sensitivity to implied volatility. Higher vega means the option price changes more when volatility changes.
8 Greeks Surface
Visualize how delta changes across stock price and time.
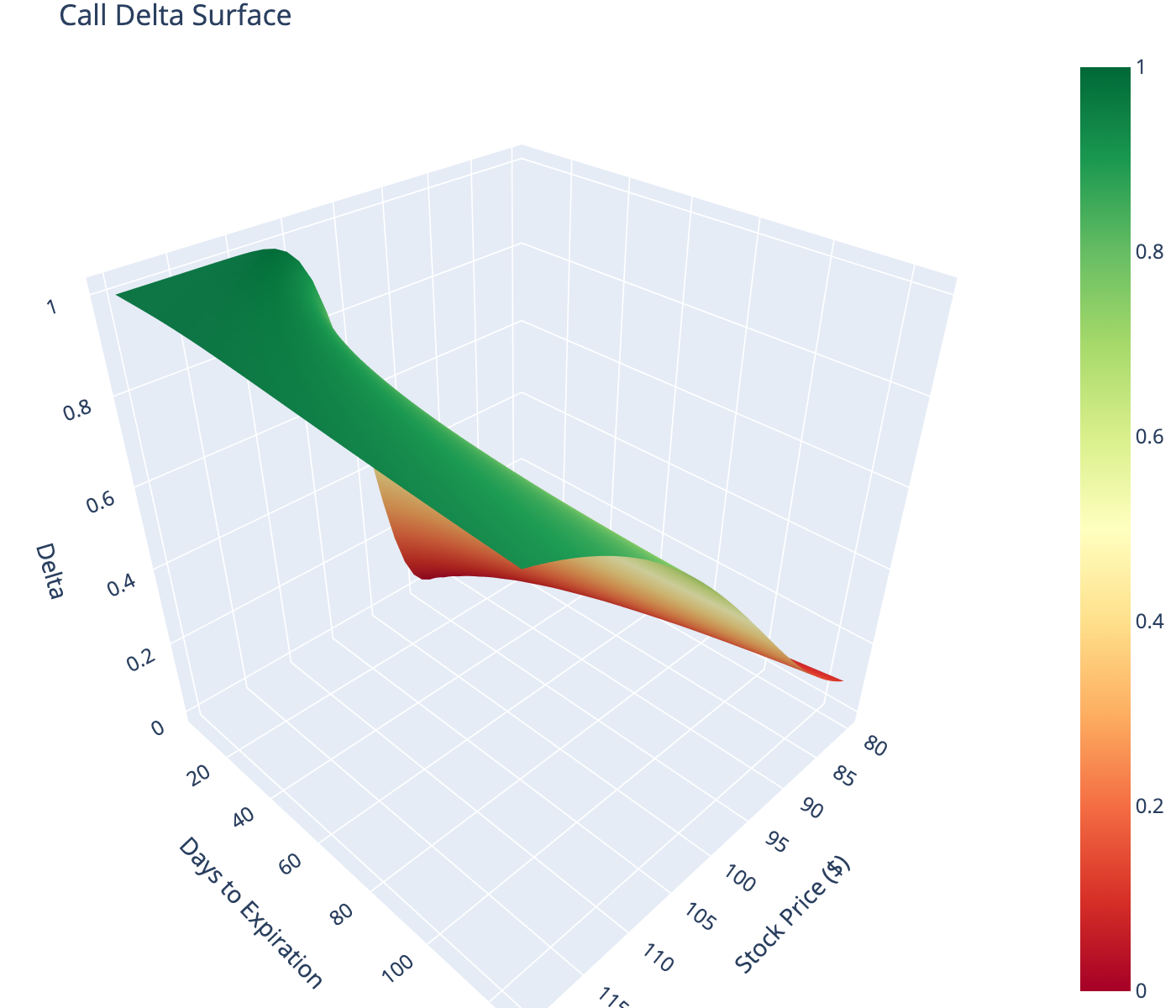
9 Delta Hedging
A delta-neutral portfolio has zero delta, meaning small price moves don’t change its value.
Position: Short 100 call options
Call Delta: 0.5695
Position Delta: -5695
Shares to Buy for Hedge: 5695
Net Delta: 010 Greek Profiles by Moneyness
| Moneyness | Price | Delta | Gamma | Theta | Vega | |
|---|---|---|---|---|---|---|
| 0 | ITM (K=90) | 11.6701 | 0.8904 | 0.0188 | -0.0209 | 0.0938 |
| 1 | ATM (K=100) | 4.6150 | 0.5695 | 0.0393 | -0.0287 | 0.1964 |
| 2 | OTM (K=110) | 1.1911 | 0.2183 | 0.0295 | -0.0190 | 0.1474 |
11 Conclusion
The Greeks provide a comprehensive view of option risk exposures:
- Delta: Directional risk, primary hedge ratio
- Gamma: Convexity risk, measures hedge stability
- Theta: Time decay, cost of holding options
- Vega: Volatility risk, key for vol trading
- Rho: Interest rate risk, usually smallest
Professional options traders monitor Greeks continuously and construct positions to achieve desired risk profiles. Understanding Greeks is essential for hedging, risk management, and designing options strategies.