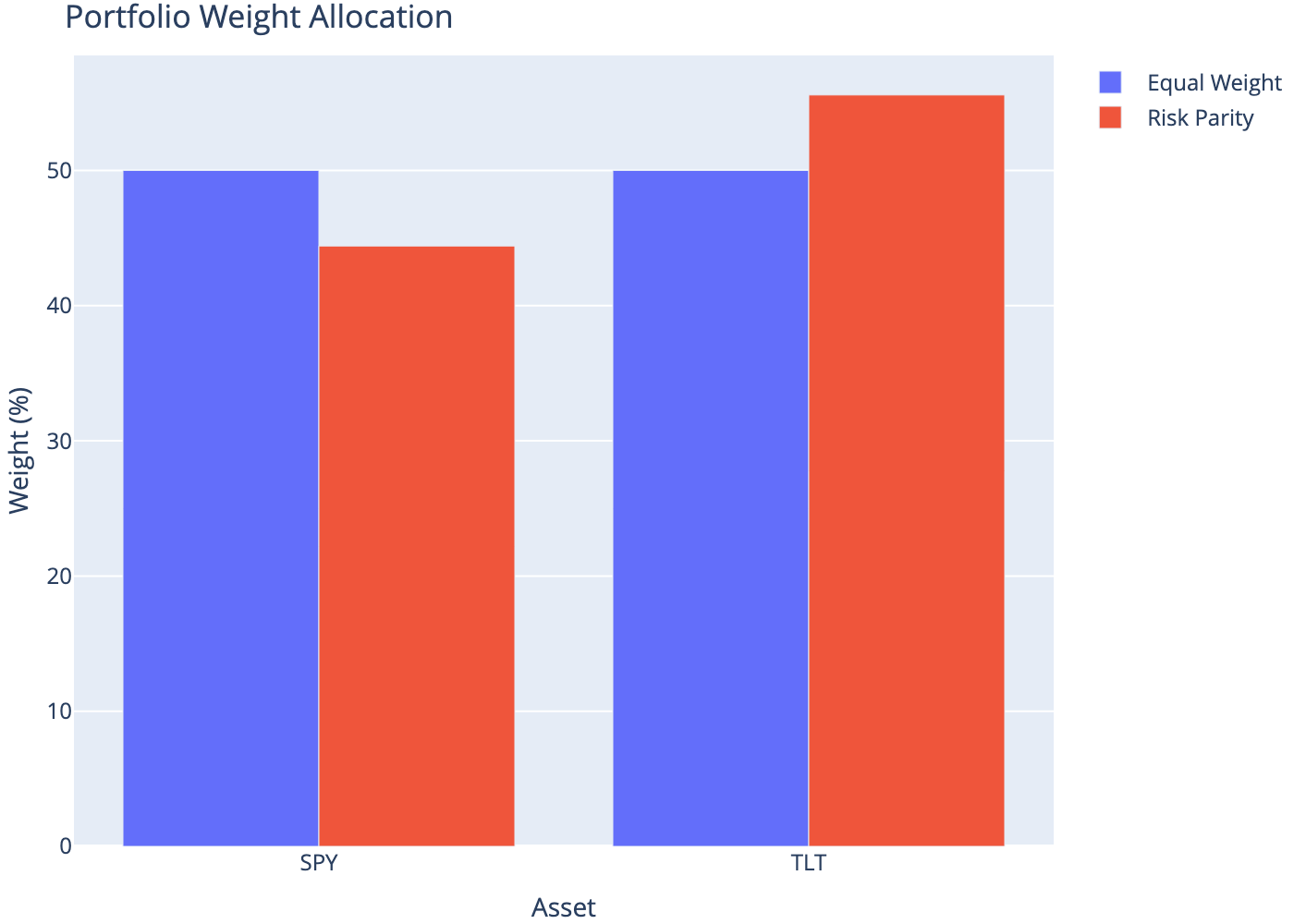
| Ticker | Ann. Volatility (%) | Risk Parity Weight (%) | |
|---|---|---|---|
| Ticker | |||
| SPY | SPY | 16.27 | 44.41 |
| TLT | TLT | 13.00 | 55.59 |
Risk Parity
Portfolio allocation based on equal risk contribution
1 Abstract
Risk Parity is a portfolio allocation strategy where each asset contributes equally to the total portfolio risk. Unlike equal-weight portfolios (where each asset receives equal capital), risk parity allocates less capital to high-volatility assets and more capital to low-volatility assets. This approach was popularized by Bridgewater Associates’ “All Weather” fund and formalized by Qian (2005).
2 Definitions
Consider a portfolio of \(n\) assets with weights \(w_i\) where \(\sum_{i=1}^{n} w_i = 1\).
For the simplified case (assuming uncorrelated assets), the inverse volatility weighting formula is:
\[ w_i = \frac{\frac{1}{\sigma_i}}{\sum_{j=1}^{n} \frac{1}{\sigma_j}} \]
Where \(\sigma_i\) is the standard deviation (volatility) of asset \(i\).
For a two-asset portfolio (assets A and B):
\[ w_A = \frac{\frac{1}{\sigma_A}}{\frac{1}{\sigma_A} + \frac{1}{\sigma_B}} = \frac{\sigma_B}{\sigma_A + \sigma_B} \]
\[ w_B = \frac{\frac{1}{\sigma_B}}{\frac{1}{\sigma_A} + \frac{1}{\sigma_B}} = \frac{\sigma_A}{\sigma_A + \sigma_B} \]
Note: This simplification assumes zero correlation between assets. For correlated assets, the full covariance matrix must be considered (Maillard et al., 2010).
3 Theoretical Example
Given two assets with annualized volatilities:
- Asset A: \(\sigma_A = 4.50\%\)
- Asset B: \(\sigma_B = 1.62\%\)
Applying the inverse volatility formula:
\[ w_A = \frac{1.62}{4.50 + 1.62} = \frac{1.62}{6.12} \approx 26.47\% \]
\[ w_B = \frac{4.50}{4.50 + 1.62} = \frac{4.50}{6.12} \approx 73.53\% \]
The higher-volatility asset (A) receives less capital, while the lower-volatility asset (B) receives more.
4 Compute (Python)
We apply risk parity to a classic stock-bond portfolio using SPY (S&P 500 ETF) and TLT (20+ Year Treasury Bond ETF).
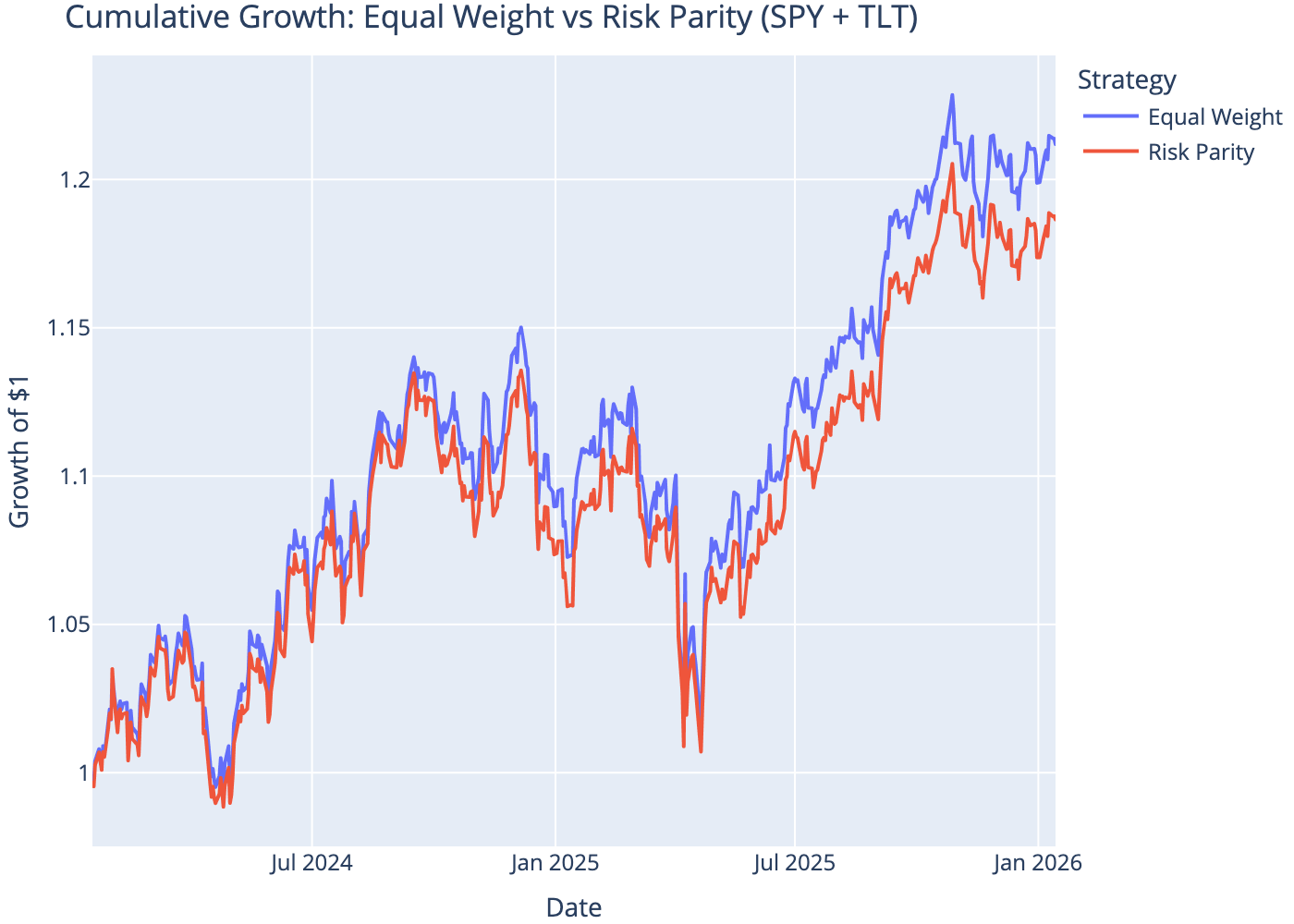
5 Comparison: Equal Weight vs Risk Parity
| Portfolio | Ann. Return (%) | Ann. Volatility (%) | Sharpe Ratio | |
|---|---|---|---|---|
| 0 | Equal Weight | 10.25 | 10.78 | 0.95 |
| 1 | Risk Parity | 9.16 | 10.59 | 0.87 |
6 Portfolio Performance
7 Weight Allocation
8 Conclusion
Risk parity allocates capital inversely proportional to volatility, ensuring each asset contributes similar risk to the portfolio. In a stock-bond portfolio, this typically results in overweighting bonds (lower volatility) relative to stocks (higher volatility). This approach often achieves lower portfolio volatility and improved risk-adjusted returns compared to equal-weight allocations.