Returns & Volatility

Computing log returns and annualized volatility

A foundational note on log returns, volatility measurement, and return distributions for liquid assets.

1 Abstract

This note computes log returns, annualized volatility, and visualizes the distribution for a liquid asset.

2 Definitions

Given a price series \(P_t\), the log return is:

\[ r_t = \ln\left(\frac{P_t}{P_{t-1}}\right) \]

Annualized volatility (assuming 252 trading days):

\[ \sigma_{\text{ann}} = \sqrt{252} \cdot \text{std}(r_t) \]

3 Compute (Python)

	ticker	period	mu_daily	mu_ann	sigma_daily	sigma_ann	n_obs
0	SPY	2y	0.000792	0.199663	0.010246	0.162653	501

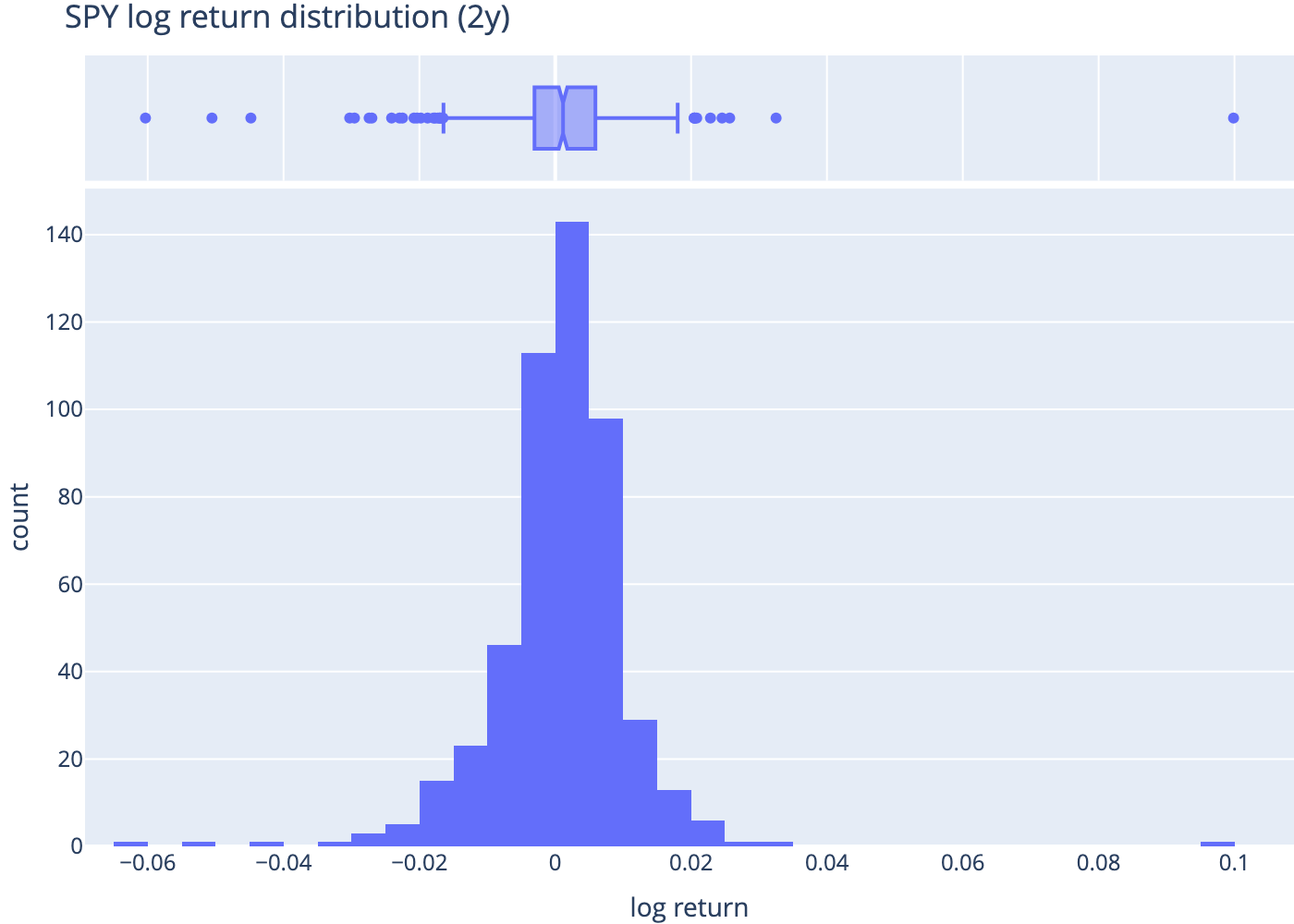
4 Distribution